January 12th, 2017
前提
每週五是我們公司的資料科學家讀書會時間,常常這類時間我可能都會在外面跟客戶開會無法參加. 但是這個禮拜總算把時間空出來參加,還好聽得懂內容跟為何要這麼做,所以相當的開心.
本週分享的是 Clustering 中的 K-Means , K-Means++ 與 \(K-MC^2\) 也就是有名的文章 K-MC2: Approximate K-Means++ in Sublinear Time
其中 K-MC2 : K-Means++ with Markov chain Monte Carlo.
簡單筆記
- Fast and Provably Good Seeding for means
- K-mean
- 計算 k-gram 之間距離
- 如果以三角形來說 tri-gram
- 透過”三角不等式”
-
第三邊不小於 1 - 2 -
第三邊不能大於 1+ 2
-
- 透過這樣來限縮第三邊的範圍可以加速 k-means 運算
- K-mean++
- 解決 k-mean 容易因為初始值導致 clustering 效果不佳
- 透過修正取點的方式(比較遠的比較容易被取到) 透過機率性的方式
- 取點只做第一次,後面還是使用 k-mean 來計算
- MCMC Samling (K-MC2)
- 在做 clustering 中心點取樣的時候
- 透過取樣後 clustering 中心點,然後來分群
- 透過 Markov Chain
- [優點]
- 以往做 K-mean 挑點,需要 k * m
- 透過這個方式可以不在需要把每個點都走過挑選
- K-mean
思考脈絡與筆記
- K-Means
- 優點:
- 分群效能快,取樣隨便取.
- 缺點:
- 精準度不足,當一開始的取樣點不好的時候.需要不斷重新取樣來重新計算.
- 優點:
- K-Means++
- 優點(解決 K-Means 問題):
- 分群精准度好
- 缺點:
- 取樣的時間複雜度變高.試著每次取樣比較遠的點.
- 優點(解決 K-Means 問題):
- K-MC2
- 優點(解決 K-Means++ 問題):
- 分群精準度好之外,也減少了取樣的複雜度.
- 缺點:
- 需要Markov Chain length 超過一定比例的 m
- 你的精準度,就會達到 K-Means++
- 優點(解決 K-Means++ 問題):
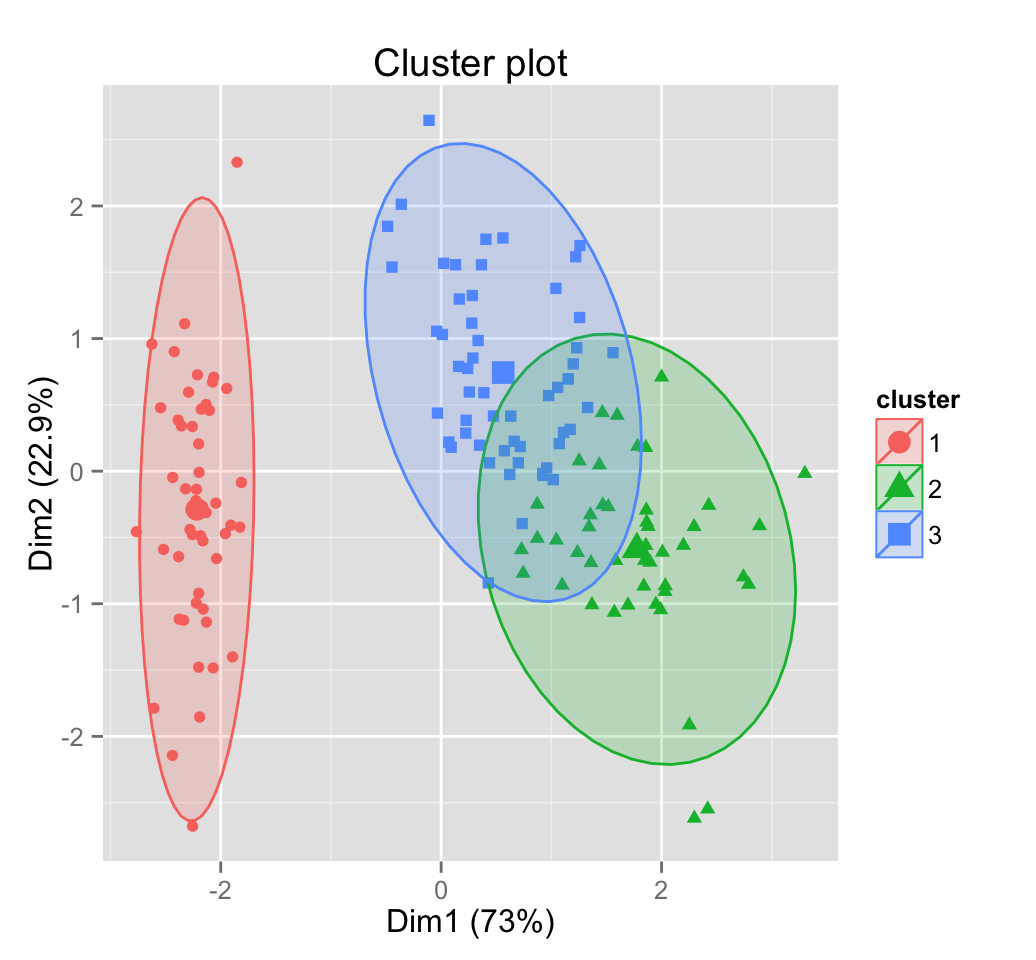
圖表
| K-Means | K-Means++ | K-MC2 | |
|---|---|---|---|
| 取樣效率 | 快 | 慢 | 中 |
| 精準度 | 當初取點錯誤,精準度就差 | 解決取點精準度問題,但是構成取點效率差 | 當 MCMC 長度 m 夠大的時候,精準度就跟 K-Means++ 一樣精準 |
| 取樣方式 | 隨機選 | 透過全部距離計算,高機率選取到比較遠的點 | 透過 MCMC 的方式,來解決 Sample 點是否要繼續來計算距離.某些機率下,不在繼續計算距離而直接移到下一個節點來計算距離. |
代碼 github.com/obachem/kmc2 :
安裝
pip install numpy
pip install kmc2
不過… macOS 會報錯
kmc2.c:232:10: fatal error: 'numpy/arrayobject.h' file not found
#include "numpy/arrayobject.h"
^
1 error generated.
error: command 'clang' failed with exit status 1
解決方式
export CFLAGS="-I /usr/local/lib/python2.7/site-packages/numpy/core/include $CFLAGS"
範例
import kmc2
import numpy
X = numpy.random.random((3, 3))
seeding = kmc2.kmc2(X, 5) # Run k-MC2 with k=5
