[Coursera][Automata] 自動機理論-Automata筆記-第三週: Context-Free Grammars and Pushdown Automata

前言與心得整理

進入到第三週，前兩個章節都是在介紹可以透過RE(Regular Expression)來表示的語言．這一次就是無法透過RE來表示的語言(CFG: Content-Free Grammar)還有相關的定義與運算．

相關文章

• [Coursera][Automata] 自動機理論-Automata筆記-第一週Finite Automata
• [Coursera][Automata] 自動機理論-Automata筆記-第二週: Regular Expression
• [Coursera][Automata] 自動機理論-Automata筆記-第三週: Context-Free Grammars and Pushdown Automata
• [Coursera][Automata] 自動機理論-Automata筆記-第四週: Pushdown Automata and Properties of Context-Free Languages
• [Coursera][Automata] 自動機理論-Automata筆記-第五週: Turing Machines and Undecidability
• [Coursera][Automata] 自動機理論-Automata筆記-第六週(上): Intractable Problems and NP-completeness
• [Coursera][Automata] 自動機理論-Automata筆記-第六週(下): Intractable Problems and NP-completeness

第三週課程內容:

Context-Free Grammar

Content-Free Grammar(以下簡稱CFG) 是一種可以透過符號來敘述語言，可以表達比RE更多的語言(但是不是全部)．特別是在表現巢狀結構的語言．

以下只介紹正式的定義:

• Terminals: 定義好的符號，類似語言中的alphabet．
• Variables: 又稱為non-terminals，有限集合的符號，另一種表示語言的方式．
• Start Symbol:類似於RE中的start state．
• Production(投射): 也就一種對應的關係，通常表示為 ->． 其中左邊是 variables 右邊是 terminals跟variables的字串． ex: S-> {0, 1}
• Derivations(推導): 主要就是將CFG由start symbol開始，並且開始將variable投射出相對應的variables或是terminals其中的代表符號是=>．
  • S->01 S->0S1 則 S=>0S1(將S->0S1)=>00SS11(將一個S->0, 另一個S->1)=>000111
• Iterated Derivation: 符號為 =>* 如同Kleene Star定義一樣，這個代表推導為0或是更多．
  • a =>* a (就是代表任意個a)
  • a =>* b and b=> c 則 a=>* c
• Sentential Forms (句型): 指的是字串可以由Start Symbol加上 terminal 或是 variables．
  • S =>* a 那麼 a就可以被稱為 sentential form (因為a是一start symbol，而且加上variable a組合而成．)

以下是一個簡單的範例:

CFG : { 0^n 1^n | n >=1 }

• terminals: {0, 1}
• variables: {S}
• start symbol: S
• product: S -> {01} S -> 0S1
• 關於Iterated Derivation範例:
  • S -> 01; S->0S1
  • 則 S=> 0S1 => 00S11 => 000111
  • 由前面的式子推導出來， S可以推導出 S或是沒有S 所以 S =>*S
    • 於是 S =>* S =>* 0S1; S=>* 00S11 ; S=>* 000111

Backus-Naur Form

程式語言的語法，通常會被寫成BNF(Backus-Naur Form)．這裡會開始把CFG的一些定義轉換到BNF上面，才能方便我們開始用在程式語言上面．

• 變數(variables)寫在 <...>裡面
• Terminal通常會用粗體或是底線
• ::= 就是代表 CFG裡面的production ->
• | 就是 OR
• 如果symbol緊接著...:代表 Kleene Star (*)的意思
• 如果是...在輸入{}之後，代表有更多的輸入． (類似function parameter裡面的 ...)

範例:

L -> a[{ab} ...] 開始推導:

• L -> aB ; B=[{ab}…]

• L-> aB ; B-> C

  ε; C={ab}… (其中 [{ab}...]代表出現 0或是以上個 {ab} 所以先用ε替代出0) 而 {ab}...代表的就是 1個或是以上

• L-> aB ; B-> C

  ε; C=AC; A={ab} (由於出現 {ab}… 一個或以上，可以用符號 C->AC 因為 A={ab} C可以繼續推導出A或是AC)

• 解答就是 L->aB B->C

  ε C->AC A->{ab}

關於 Derivation的順序(Leftmost or Rightmost)

根據定義，其實BNF可以是Leftmost 也可以是 Rightmost．但是必須要在Derivation上面寫清楚．

    L ->_lm A[{ab}...] (_lm代表 leftmost 左邊作為優先順序)

Parse Tree

定義

• Parse Tree:是拿來表達CFG的樹狀結構，其中:
• 根節點(root): 為CFG中的Start Symbol
• 葉節點(Leaves): 一定都是terminals或是ε
• 中間節點(iterate node): 可以是variable或是terminals

(image from Coursera Automata Course)

以上是一個範例圖形，主要是敘述 S-> SS | (S) | ()，可以看出來:

• 葉節點一定為(或是)，必須要中間節點才會出現Variable S
• Start Symbol 也就是Root 是 S
• 其中的yield為此parse tree的trabersal 結果 yield : ( () ) ()

Leftmost Induction 與 Rightmost Indction

如果要用Leftmost Induction的順序來分析Parse Tree:

範例:

• Induction: Xi =>*_lm Wi
• Start Symbol: A
• 於是乎:
  • A=>_lm X1 X2 X3 … Xn
  • A=>_lm W1 X2 X3 … Xn (將Xi換為W1)
  • A=>_lm W1 W2 W3 … Wn
  • 最後的結果為 W1 W2 … Wn

Ambiguity Grammars

其實就是簡單指有 |的 grammar 比如說 S-> S | {S}就是．

範例：

    B-> (RB|ε  R-> )| (RR

一開始會覺得這個很難解讀，甚至完全不瞭解該如何解讀這段題目．其實他應該要拆解成兩段敘述:

• B-> (RB|ε 代表的是 B 可以推導出 (RB 或是 ε (代表結束)
• R-> ) | (RR 代表 R可以推導出 ) 或是 (RR

透過課堂給的範例，我們來跑一次

    B-> (RB|ε  R-> )| (RR
            
    Input: (()) ()

分析的流程如下(走Leftmost方式):

• 一開始從 B開始
• 輸入(:
  • 能找到的只有 B-> (RB 於是替換成 (RB
• 輸入(:
  • (RB 將其中的 R替換成 (RR 於是結果是 ((RRB
• 輸入):
  • ((RRB 將其中的R(由於是Leftmost，所以是挑左手邊第一個R) 換成 ) ，於是結果是 (()RB
• 輸入):
  • (()RB 跟上一步一樣，改成 (())B

….之後分析方式都一樣． 最後結果是 (())()．

Derive Nothing

這裏是指CFG有可能造成持續有variable而無法完全轉換成symbol的狀態．拿以下的例子: 注意: 大寫字母是Variable，小寫字母代表是Symbol

    S -> AB | C, A -> aA | a, B-> bB, C -> c

由這個例子可以看到:

• 由start symbol S -> AB之後， A 可以透過 aA 或是在轉換成 a來轉換成symbol (這裏稱為reach symbol)．
• 但是 B -> bB 於是持續有個variable B存在．
• 這樣的CFG無法轉換出全部symbol的語句．

Elimilate Variable

這裏主要是消除一些造成Derive Nothing的grammar，在上面的例子：

    `B -> bB` 

會造成無窮的variable B產生，所以我們必須要把B消除掉．

    S -> A|C, A-> aA | a, C->c

這樣就能確保能夠Derive Symbol．

Nullable Symbol

所謂的Nullable Symbol指的是某些Variable會推導出ε(epsilon)．也就是說 A->ε，同時我們也稱為A->ε這樣的production叫做ε-productions．舉例來說:

            S -> AB | C, A -> aA | ε, B-> bB | A, C -> c

• 根據以上的例子 A -> aA | ε所以我們可以說 A 是 Nullable Symbol．
• 由於 B-> bB | A．所以 B->A->ε． B 也是Nullable Symbol
• 推導出 S->AB 所以 S -> AB -> εε．S也是Nullable Symbol

Elimilate ε-Productions

由於 ε-productions會產生出Nullable Symbol．所以我們必須要把會產生ε-productions的grammar消除掉．使用的流程如下:

    S -> ABC,  A-> aA|ε , B-> bB | ε , C-> ε

• 由於推導出 A->ε B->ε C->ε 導致 S -> ε．
• 找出新的grammars 透過S找出所有會找出epsilon變數(以這個為例: S, A, B ,C 都是，但是如果S->ABCD, D->d 的話就不需要找D的宇集合)的宇集合，並修改如下

  • S -> ABC

    AB

    AC

    BC

    A

    B

    C

  • A-> aA (已經把ε去除)
  • B->bB (已經把ε去除)
  • C -> ε (先不去除ε等等要拿來消去grammar)
• 去除掉所有的ε-productions，由於剩下 C -> ε，消去所有跟C有關的Grammar
• 結果如下:

  • S -> ABC

    AB

    AC

    BC

    A

    B

    C

  • 推導出 S -> AB

    A

    B

  • A-> aA
  • B->bB

Unit Production 跟 Pair

Unit Production 指的是grammar剛好能夠 product 到一個variable． 也就是 A => * B．所以 S=>* S, A=>*A．

Pair A, B 寫成(A, B)代表存在著unit production A=>*B．

Pair同時具有遞移律，如果 (A, B)且 (B, C)則我們必定能夠找到 A=>*B , B=>*C 根據law of induction必定能夠推導出 A=>*C．所以也存在著 (A, C)．

範例:

    S→AB|Aa; A→cD; B→aCb|C|A; C→D; D→a|b|c  
    找出所有的pair               

• 一開始就能得知，必定存在著 (S, S), (A, A) (B, B) (C,C) (D, D)
• 接下來要找unit production可以找到 B->C B->D B->A C->D 於是我們取得 (B, D), (B, D), (B,A) (C, D)
• 所有的Pair 即為(S, S), (A, A) (B, B) (C,C) (D, D)(B, D), (B, D), (B,A) (C, D)

Cleaning Up a Grammar

所謂的Cleaning Up grammar就是必須要消除:

• No useless symbol
• No ε-Productions
• No Unit Productions

Chomsky Normal Form

CFG 如果滿足以下兩個條件，可以被稱為是CNF(Chomsky Normal Form):

• 只存在兩個variable在body A->BC
• 或是只存在一個terminal A->a

• 或是 S->ε

    定理: L 是CFG，L-ε必定存在一個CFG是屬於CNF (L- ε 代表語言減去ε之後的其他集合)
  

這個定理也表示，任何的CFG(除了ε)一定都可以轉換成CNF的格式．

舉例

    A->BCDE

• 先轉換成 A-> BF, F->CDE
• A->BF, F->CG G->DE 即完成

Pushdown Automata

Pushdown Automata(PDA)主要是透過stack來存放某些symbol(可能是代表marker或是狀態，不侷限)．其實整體架構不難，只是何時要把symbol push進stack何時需要把symbol pop就是靠原本的定義．

• 類似Pushdown Automata wiki用更多個參數的宣告來表示push/pop

(圖片來自課堂 Automata Course)

範例:

在這樣的宣告下，這個PDA主要是幫助我們檢查全部的輸入(input)中，0與1的個數是否成對．

基本宣告如下:

• PDA 可以接受 { 0^n 1^n | n>=1 }
• q是start state
• 輸入為1的時候會走到 p state並且pop
• f 是 final state
• 關於symbol 的宣告:
  • Z 代表stack 底部，代表1與0的個數相同．
  • X 代表一個0輸入，每輸入一個0, 就push 一個X進stack
• 關於transition function 的表示
  • δ(q, 0, Z)={(q,Z)} 代表從q 狀態開始，輸入為0，其中symbol為Z． {(q,Z)} 左邊代表透過input 0所走到的狀態q，右邊代表stack狀態有一個Z．
  • δ(q, 0, X)={(q,XZ)} 代表從繼續從q出發輸入0，到達q．其中stack為ZX
  • δ(q, 1, X)={(p,Z)} 代表從繼續從q出發輸入1，到達p．其中stack為Z．注意第三個參數會提到要pop X．

ID: Instantaneous Descriptions

ID: Instantaneous Descriptions是一個算式可以幫助我們知道總共輸入多少，進行到哪個階段，並且也顯示stack狀態的一個算式．

(q, w, a) 其中q代表目前狀態，w代表剩下的輸入，a代表stack狀態(top在左邊)．

其中每個ID之前或用一個 “Goes-To”(符號沒有了 XD要用圖形) 符號代表下一個推導．

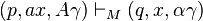
範例

• (q, 000111, Z) “Goes-To”
• (q, 00111, XZ) 輸入一個0並且放入一個X到stack頂端
• (q, 0111, XXZ) 輸入一個0並且放入一個X到stack頂端
• (q, 111, XXXZ) 輸入一個0並且放入一個X到stack頂端
• (q, 11, XXZ) 輸入一個1並且從stack頂端移走一個X
• (q, 1, XZ) 輸入一個1並且從stack頂端移走一個X

**如何判斷輸入的字串有沒有被PDA所接受? **

• 確認 ID最後stack為狀況為Z並且狀態走到f 也就是整個ID為 (f, ε, Z)

程式作業

主要是實作 RE -> ε-NFA的程式． 其實大部分已經都完成好了，主要是考觀念關於 union， concatenation跟 closure 大概五分鐘就搞定（如果概念沒問題的話….)，基本觀念重新敘述如下:

• union: ex: A union B
  • 主要是會產生兩個新的狀態，
  • 新的start state分別連到原先 A start state 與 B start state．
  • 新的fianl state分別會被A與B的final state所連接．
  • 連接的輸入都是 ε

• concatenation: ex: A concatenation B
  • 主要是將A與B的圖形連接，A的final state會連到B的start state
  • 當然連接的輸入都是 ε

• closure: ex: Closure(A)
  • Closure 主要就是要將幾個ε-translation function 加上去
  • 建立兩個新的狀態
  • new start -> orignal start
  • orignal final -> new final
  • final->start
  • new start -> new final
  • 當然連接的輸入都是 ε

其實可以參考slide 5 (14~16) 主要就是把這三個部分實現出來．

相關程式

本週雖然課堂都在講CFG的部分，但是程式的部分先試著把 ε-NFA完成． 程式碼在這裡 https://github.com/kkdai/e-nfa

幾個註解:

• Epsilon-NFA 其實不難實現，主要是走完input到每一個(guess)猜想狀態後，需要將自己所有擁有的ε路徑(也就是輸入的input為空)把他再走一次．
• 而ε的input也是需要有輸入才能知道ε要走到那些states

參考網址

• Coursera: Automata Course
• Context-free_grammar:wiki
• CNF: Chomsky Normal Form
• Pushdown Automata