[中文導讀] Facebook 的時間序列資料庫 - Gorilla (Gorilla: A Fast, Scalable, In-Memory Time Series Database)

May 18th, 2016

(come from Paper)

前言:

本文會介紹最近被討論的 Facebook 時間序列資料庫的論文，並且會介紹資料庫壓縮演算法．其中不少解讀都是參考 Morning Paper 裡面的論文導讀．

最後會導入 Damian Gryski 根據論文推導出的演算法 dgryski/go-tsz ．

原始論文:

Gorilla: A Fast, Scalable, In-Memory Time Series Database

導讀:

什麼是 Gorilla ?

Gorilla 是 Facebook 開發的時間序列資料庫．其實市場上已經有很多的時間序列資料庫 (HBase on TSDB(time-series database)) ，為什麼還需要自己開發一個呢?

資料的儲存過於龐大
查詢的延遲過長

所以 Gorilla 針對這些有了以下的優化:

針對 timestamp 的壓縮
分析並且針對資料的壓縮
放在記憶體 (in-memory databse)

那麼 Gorilla 比起一般的時間序列資料庫究竟有多強大呢?

透過將時間與數值的壓縮，並且透過儲放在記憶體的操作． Gorilla 可以達到:

73 倍的 Query Latency 減少
14 倍的 Query Throughput 增加

為了要儲存到 26 小時以上的時間序列資料，並切壓縮到 1.3 TB 的記憶體之中(分散在 20 部伺服器中)．所以 Gorilla 針對儲存資料有相當程度的壓縮．

透過資料的壓縮最佳狀態可以達到:

(come from Paper)

高達 12 倍的壓縮比: 原先 16 bytes 的數值資料(包括 timestamp 與 value )透過壓縮，一般而言平均可以達到 1.37 bytes (通常在經過 240 分鐘後)

12倍的壓縮比？那麼大的壓縮比是如何做到?

簡單的來說 Gorilla 透過將時間資料( timestamp )與數值資料( value ) 的壓縮．其壓縮的方式是參考前一次的資料，透過時間序列資料庫的特性:

連續性資料
在比較小的取樣時間中，每筆資料間的變化不大

透過這樣的方式，可以拿目前的資料 \(t_n\) 去與前一筆資料 \(t_(n-1)\) 比對的方式，來拿到差異值 (delta) ．並且將差異值做一定程度的壓縮．達到整個資料庫數值的壓縮．

壓縮的演算法: 關於時間資料的壓縮

首先針對時間資料的壓縮部分，讓我們先看看以前的時間可能如何紀錄: (舉例)

\(t_0\) => 02: 00 : 00
\(t_1\) => 02: 01 : 02
\(t_2\) => 02: 02 : 02
\(t_3\) => 02: 03 : 02

如果要直接紀錄的話，其實資料長度會變得相當大．讓我們換個角度來看:

\(t_0\) => 02: 00 : 00 (跟之前差距 0)
\(t_1\) => 02: 01 : 02 (跟之前差距 62 秒)
\(t_2\) => 02: 02 : 02 (跟之前差距 60 秒)
\(t_3\) => 02: 03 : 02 (跟之前差距 60 秒)

這樣紀錄 delta 只要紀錄差異就好，那有可能更簡短嗎？

\(t_0\) => 02: 00 : 00 (跟之前差距 0)
\(t_1\) => 02: 01 : 02 (跟之前差距 62 秒)
\(t_2\) => 02: 02 : 02 (跟之前差距 60 秒，跟上一個差距的差異 -2 秒 )
\(t_3\) => 02: 03 : 02 (跟之前差距 60 秒,跟上一個差距的差異 0)

這個概念就是紀錄 delta of delta，也就是差距中的差異．

將 差距中的差異 以字母 \(D\) 來代替，透過 Tag Bit 與 Value Bits 來表示．

(Pic: from Morning Paper )

轉換之前的範例為:

\(t_0\) => 02: 00 : 00 => D = 0, tag bit 0.
\(t_1\) => 02: 01 : 02 => D = 62, tag bit 10, value 62 (011 1110) 總共 9 bits
\(t_2\) => 02: 02 : 02 => D = -2, tag bit 10, value -2 (111 1101) 總共 9 bits
\(t_3\) => 02: 03 : 02 => D = 0, tag bit 0 總共 1 bit

這樣就可以節省不少空間來儲存時間資料．

(come from Paper)

這張圖，顯示了大部分的時間資料的分佈．可以透過這張圖看到，不少的時間差異的差距 (delta of delta) 其實都是屬於 0 (具有 96%)．

也就是說經常兩兩儲存的時間差距是相同的，這樣的話其實可以不需要儲存那麼繁瑣的時間資料．而透過一個方式來儲存．

壓縮的演算法: 關於時間資料的壓縮 (程式碼)

func (s *Series) Push(t uint32, v float64) {
	s.Lock()
	defer s.Unlock()

	if s.t == 0 {
		// first point
		s.t = t
		s.val = v
		//s.T0 是第一筆時間資料
		//s.tDelta 就是前兩筆的差異
		s.tDelta = t - s.T0
		s.bw.writeBits(uint64(s.tDelta), 14)
		s.bw.writeBits(math.Float64bits(v), 64)
		return
	}

	//tDelta 就是現在的目前的時間跟上一次時間的差異
	tDelta := t - s.t
	//dod (Delta of Delta): 就是 (tn - t(n-1) ) - (t(n-1) - t(n-2) )
	dod := int32(tDelta - s.tDelta)

	//透過 dod 來放置 tag but 䢎 vakye
	switch {
	case dod == 0:
		s.bw.writeBit(zero)
	case -63 <= dod && dod <= 64:
		// 放置 tag bit
		s.bw.writeBits(0x02, 2) // '10'
		// 放置 value bit
		s.bw.writeBits(uint64(dod), 7)
	case -255 <= dod && dod <= 256:
		s.bw.writeBits(0x06, 3) // '110'
		s.bw.writeBits(uint64(dod), 9)
	case -2047 <= dod && dod <= 2048:
		s.bw.writeBits(0x0e, 4) // '1110'
		s.bw.writeBits(uint64(dod), 12)
	default:
		s.bw.writeBits(0x0f, 4) // '1111'
		s.bw.writeBits(uint64(dod), 32)
	}
	
	...

(code from https://github.com/dgryski/go-tsz/blob/master/tsz.go )

壓縮的演算法: 關於數值資料的壓縮

到數值的部分，一樣使用之前的概念．也就是 delta of delta 的概念來處理數值壓縮．而差異的部分不再使用 minus 而是透過 XOR 的方式．

(come from Paper)

將以上的資料做個簡單的 XOR 運算，來計算數值資料中的差距:

\(v_1\) 12 -> 0x40280 -> XOR: N/A
\(v_2\) 24 -> 0x40380 -> XOR: 0x00100
\(v_3\) 15 -> 0x402e0 -> XOR: 0x00160
\(v_4\) 12 -> 0x40280 -> XOR: 0x00060
\(v_5\) 12 -> 0x40280 -> XOR: 0x0

計算好各個數值資料間的 XOR 之後，我們要來針對這樣的資料壓縮:

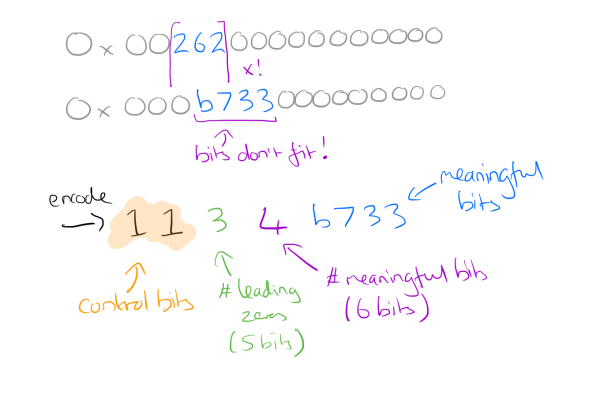
(Pic: from Morning Paper )

針對以上的圖片，主要壓縮方式如下:

假設計算數值，如下

\(v_2\) -> XOR: 0x001000000000000
\(v_3\) -> XOR: 0x001600000000000

計算各個數值 XOR 的 leading/meaning/trailing bits

\(v_2\) -> XOR: 0x001000000000000,
- leading bit: 2
- meaningful bit: 1
\(v_3\) -> XOR: 0x001600000000000
- leading bit: 2
- meaningful bit: 2

其中:

Leading Bit: 就是 XOR 遇到第一個非零數值”前”的零的個數
Meaningful Bit: 中間所有非零的個數

計算 control bit ，其規則如下:

如果 XOR 是 0, control bit = 0
如果 XOR 不是 0, control bit = 1，並且透過以下方式來計算下一個 control bit
- Leading bit, Meaningful bit 個數相同，但是其中 Meaningful 數值不同． Control Bit 0 ，接下來是 Meaningful value.
- 如果 Leading bit 跟 Meaningful 個數與數值不同， Control bit 1 ．並且接下來存放資料:
  - 5 bits: 放 Leading bit 個數
  - 6 bits: 放 Meaningful bit 個數
  - 放置所有的 Meaningful bit 數值．

拿個範例拿來做壓縮範例:

會拿以下的數值來做壓縮運算，真實數值比較大這邊只做範例：

\(v_1\) 12 -> 0x40280 -> XOR: N/A
\(v_2\) 24 -> 0x40380 -> XOR: 0x00100
\(v_3\) 15 -> 0x402e0 -> XOR: 0x00160
\(v_4\) 12 -> 0x40280 -> XOR: 0x00060
\(v_5\) 12 -> 0x40280 -> XOR: 0x0

經過計算後:

\(v_1\) : treat XOR : 0x40280
- Control bit: 11 (bit)
- Leading bit: 00000 (bit)
- Meaningful bit: 00101 (5 bit)
- Meaningful value: 0x40280
\(v_2\) : XOR : 0x00100 上一個 XOR: 0x40280
- Control bit: 11 (bit)
- Leading bit: 00000 (bit)
- Meaningful bit: 00101 -> 5 (bit)
- Meaningful value: 0x40280
\(v_2\) : XOR : 0x00160 上一個 XOR: 0x00100
- Control bit: 10 (bit)
- Leading bit: 00010 -> 2 (bit)
- Meaningful value: 0x160
\(v_4\) : XOR : 0x00060 上一個 XOR: 0x00160
- Control bit: 11 (bit)
- Leading bit: 00011 -> 3 (bit)
- Meaningful bit: 00010 -> 2 (bit)
- Meaningful value: 0x60

壓縮的演算法: 關於數值資料壓縮的程式碼:

func (s *Series) Push(t uint32, v float64) {
	...
	
	//計算 XOR 數值
	vDelta := math.Float64bits(v) ^ math.Float64bits(s.val)

	// 如果 XOR ==0
	if vDelta == 0 {
		//只寫一個 Bit `0`
		s.bw.writeBit(zero)
	} else {
		//如果是零，先寫入第一個 control bit `1`
		s.bw.writeBit(one)

		//計算 leading 跟 trailing 個數
		leading := uint8(bits.Clz(vDelta))
		trailing := uint8(bits.Ctz(vDelta))

		// clamp number of leading zeros to avoid overflow when encoding
		if leading >= 32 {
			leading = 31
		}

		// TODO(dgryski): check if it's 'cheaper' to reset the leading/trailing bits instead
		
		// leading 跟 trail 相同，但是 meaningful 數值不同
		if s.leading != ^uint8(0) && leading >= s.leading && trailing >= s.trailing {
			//寫入第二個 control bit `0`
			s.bw.writeBit(zero)
			//寫入meaningful value
			s.bw.writeBits(vDelta>>s.trailing, 64-int(s.leading)-int(s.trailing))
		} else {
			s.leading, s.trailing = leading, trailing

			//連 leading 都不相同，落入其他 case
			//寫第二個 control bit `1`
			s.bw.writeBit(one)
			//寫入 leading 個數
			s.bw.writeBits(uint64(leading), 5)

			// Note that if leading == trailing == 0, then sigbits == 64.  But that value doesn't actually fit into the 6 bits we have.
			// Luckily, we never need to encode 0 significant bits, since that would put us in the other case (vdelta == 0).
			// So instead we write out a 0 and adjust it back to 64 on unpacking.
			sigbits := 64 - leading - trailing
			//寫入 meaningful bit 個數
			s.bw.writeBits(uint64(sigbits), 6)
			//寫入 meaningful value
			s.bw.writeBits(vDelta>>trailing, int(sigbits))
		}
	}
	
	...

(code from https://github.com/dgryski/go-tsz/blob/master/tsz.go )

數值資料壓縮的成果計算:

(come from Paper)

經過論文中計算，一般而言透過 XOR 計算過後．有 59%的數值資料都會落入 0 也就是說跟前一個數值相同．另外 control bit 10 的 case 會達到 28.3 % ．最後比較長 (可能) 的 control bit 11 的 case 只有 12 % ．

這個表格也表示，透過這樣的壓縮有效的將數值資料可以做一定程度的壓縮．

心得:

這篇論文其實很棒，也是我第一篇透過 “Morning Paper” 來看懂的第一篇論文．我相信 Gorilla 對於資料壓縮的方式，對於之後如果有機會處理 Streamming Data 或是針對時間序列資料庫的處理都會有更有效率的方式．

參考

論文解讀 (5)

Evan

Attitude is everything

[中文導讀] Facebook 的時間序列資料庫 - Gorilla (Gorilla: A Fast, Scalable, In-Memory Time Series Database)

前言:

原始論文:

Gorilla: A Fast, Scalable, In-Memory Time Series Database

導讀:

什麼是 Gorilla ?

那麼 Gorilla 比起一般的時間序列資料庫究竟有多強大呢?

高達 12 倍的壓縮比: 原先 16 bytes 的數值資料(包括 timestamp 與 value )透過壓縮，一般而言平均可以達到 1.37 bytes (通常在經過 240 分鐘後)

12倍的壓縮比？ 那麼大的壓縮比是如何做到?

壓縮的演算法: 關於時間資料的壓縮

壓縮的演算法: 關於時間資料的壓縮 (程式碼)

壓縮的演算法: 關於數值資料的壓縮

計算各個數值 XOR 的 leading/meaning/trailing bits

計算 control bit ，其規則如下:

拿個範例拿來做壓縮範例:

壓縮的演算法: 關於數值資料壓縮的程式碼:

數值資料壓縮的成果計算:

心得:

參考

Share Post

Evan

12倍的壓縮比？那麼大的壓縮比是如何做到?